Rappels d'Algèbre Linéaire

Séance 5 : Rappels d'Algèbre Linéaire

➗ Vecteurs

Un vecteur est un concept fondamental en mathématiques, en physique et en ingénierie, représentant une quantité possédant à la fois une magnitude (ou norme) et une direction. Il est souvent visualisé comme une flèche dans l'espace, indiquant une direction spécifique et une longueur proportionnelle à sa magnitude.

🧭 Représentation géométrique

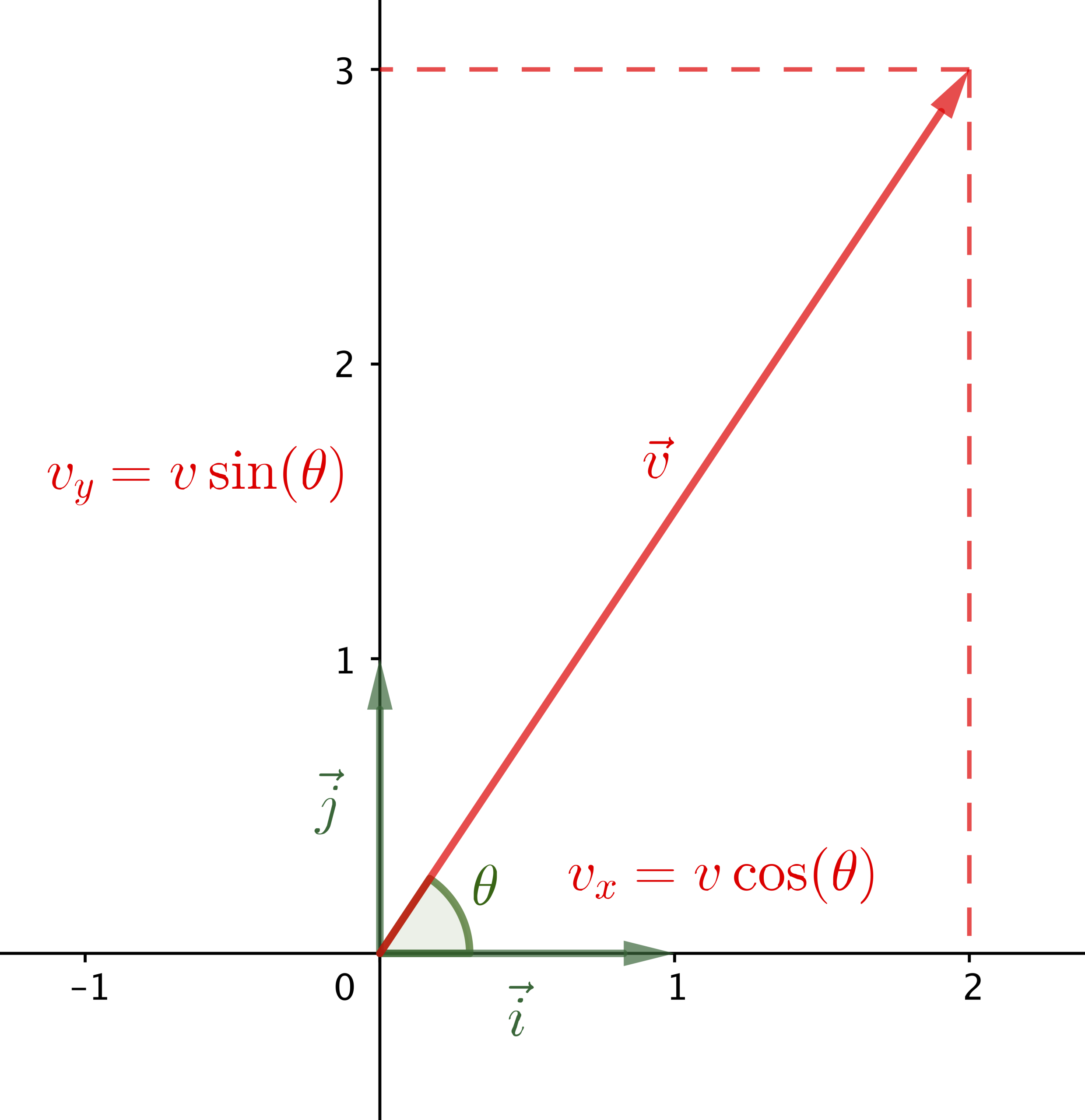
Dans un espace euclidien, un vecteur est représenté par un segment orienté, c'est-à-dire une flèche allant d'un point A (origine) à un point B (extrémité). Ce vecteur, noté \(\vec{AB}\), est défini par trois caractéristiques principales :

• Direction : la droite (AB) sur laquelle le vecteur est aligné
• Sens : de A vers B
• Norme : la longueur du segment [AB], représentant la magnitude du vecteur

Il est important de noter que la position du vecteur dans l'espace n'affecte pas ses propriétés intrinsèques. Deux vecteurs ayant la même direction, le même sens et la même norme sont considérés comme égaux, même s'ils sont situés à des endroits différents.

🧮 Représentation algébrique

Dans un espace vectoriel, un vecteur est souvent représenté par une liste ordonnée de nombres réels, appelés composantes. Par exemple, dans un espace à trois dimensions, un vecteur \(\vec{v}\) peut être représenté par :

\[ \vec{v} = \begin{pmatrix} v_1 \\ v_2 \\ v_3 \end{pmatrix} \]

où \(v_1\), \(v_2\) et \(v_3\) sont les composantes du vecteur selon les axes x, y et z, respectivement.

Ces composantes permettent de réaliser des opérations algébriques telles que l'addition de vecteurs, la multiplication par un scalaire, et le calcul du produit scalaire ou vectoriel.

🔄 Opérations sur les vecteurs

• Addition : l'addition de deux vecteurs consiste à additionner leurs composantes respectives.
  \[ \begin{pmatrix} a_1 \\ a_2 \end{pmatrix} + \begin{pmatrix} b_1 \\ b_2 \end{pmatrix} = \begin{pmatrix} a_1 + b_1 \\ a_2 + b_2 \end{pmatrix} \]
• Multiplication par un scalaire : multiplier un vecteur par un nombre réel (scalaire) revient à multiplier chacune de ses composantes par ce nombre.
  \[ \lambda \begin{pmatrix} v_1 \\ v_2 \end{pmatrix} = \begin{pmatrix} \lambda v_1 \\ \lambda v_2 \end{pmatrix} \]
• Produit scalaire : le produit scalaire de deux vecteurs est un nombre réel obtenu en multipliant leurs composantes correspondantes et en les additionnant.
  \[ \vec{u} \cdot \vec{v} = u_1 v_1 + u_2 v_2 + u_3 v_3 \]
• Produit vectoriel : le produit vectoriel de deux vecteurs dans l'espace tridimensionnel est un vecteur perpendiculaire aux deux vecteurs initiaux, dont la direction est déterminée par la règle de la main droite et la magnitude par la formule :
  \[ \|\vec{u} \times \vec{v}\| = \|\vec{u}\| \cdot \|\vec{v}\| \cdot \sin(\theta) \]
  où \(\theta\) est l'angle entre les vecteurs \(\vec{u}\) et \(\vec{v}\).

🌐 Applications des vecteurs

Les vecteurs sont omniprésents dans de nombreux domaines :

• Physique : représentation de forces, vitesses, accélérations, champs électriques et magnétiques
• Géométrie : définition de droites, plans, translations et rotations
• Informatique : modélisation graphique, calculs en 3D, intelligence artificielle
• Économie : analyse de portefeuilles financiers, modélisation de données multidimensionnelles

🧩 Vecteurs et espaces vectoriels

Un espace vectoriel est un ensemble de vecteurs qui peut être combiné linéairement, c'est-à-dire que l'on peut effectuer des opérations d'addition et de multiplication par un scalaire tout en restant dans l'ensemble. Les vecteurs dans un espace vectoriel respectent certaines propriétés, telles que :

• La commutativité \(\vec{u} + \vec{v} = \vec{v} + \vec{u}\)
• L'associativité \(\vec{u} + (\vec{v} + \vec{w}) = (\vec{u} + \vec{v}) + \vec{w}\)
• L'existence d'un vecteur nul \(\vec{u} + \vec{0} = \vec{u}\)

Les vecteurs peuvent également être généralisés en tenseurs, qui sont des objets mathématiques représentant des relations linéaires entre des vecteurs, des scalaires et d'autres tenseurs. Un vecteur est un tenseur d'ordre 1, tandis qu'une matrice est un tenseur d'ordre 2.

➗ En conclusions

Un vecteur est un objet mathématique représenté par une liste ordonnée de nombres (scalaires) qui peut être interprété comme une direction et une magnitude dans l'espace.

x₁

x₂

⋮

xₙ

Opérations sur les vecteurs

Addition vectorielle

u + v = (u₁+v₁, u₂+v₂, ..., uₙ+vₙ)

Addition composante par composante

Multiplication par scalaire

α·v = (α·v₁, α·v₂, ..., α·vₙ)

Chaque composante est multipliée par le scalaire α

Produit scalaire

u·v = ∑(uᵢ·vᵢ) = u₁v₁ + u₂v₂ + ... + uₙvₙ

Produit des composantes puis somme

Norme (longueur)

||v|| = √(v·v) = √(v₁² + v₂² + ... + vₙ²)

Distance euclidienne depuis l'origine

✖️ Matrices

Une matrice est un tableau rectangulaire de nombres disposés en lignes et colonnes. Les matrices sont fondamentales pour représenter des transformations linéaires.

a₁₁

a₁₂

⋯

a₁ₙ

a₂₁

a₂₂

⋯

a₂ₙ

⋮

⋮

⋱

⋮

aₘ₁

aₘ₂

⋯

aₘₙ

Opérations sur les matrices

Addition matricielle

A + B = [aᵢⱼ + bᵢⱼ]

Addition élément par élément (mêmes dimensions)

Multiplication par scalaire

α·A = [α·aᵢⱼ]

Chaque élément est multiplié par α

Produit matriciel

(AB)ᵢⱼ = ∑(aᵢₖ·bₖⱼ)

Nombre de colonnes de A = nombre de lignes de B

Transposition

Aᵀ = [aⱼᵢ]

Échange des lignes et colonnes

🔢 Propriétés Importantes

Propriétés des opérations vectorielles

• Commutativité: u + v = v + u
• Associativité: (u + v) + w = u + (v + w)
• Distributivité: α(u + v) = αu + αv
• Produit scalaire: u·v = v·u
• Bilinéarité: (αu + βv)·w = α(u·w) + β(v·w)

Propriétés des opérations matricielles

• Associativité: (AB)C = A(BC)
• Distributivité: A(B + C) = AB + AC
• Non-commutativité: AB ≠ BA (en général)
• Transposition: (AB)ᵀ = BᵀAᵀ
• Matrice identité: AI = IA = A

🧮 Applications en Machine Learning

L'algèbre linéaire est fondamentale pour le Machine Learning et le Deep Learning :

Exemples d'applications

• Régression linéaire: Résolution par moindres carrés (XᵀX)⁻¹Xᵀy
• PCA: Réduction de dimensionnalité via décomposition en valeurs propres
• Réseaux de neurones: Propagation avant/arrière comme produits matriciels
• Word Embeddings: Représentation des mots comme vecteurs
• Computer Vision: Transformations d'images comme opérations matricielles

Propagation avant dans un réseau de neurones:
aⁱ⁺¹ = σ(Wⁱaⁱ + bⁱ)