Neurosciences Computationnelles : Le Perceptron

🧠 Qu'est-ce qu'un Perceptron ?

Le perceptron, introduit par Frank Rosenblatt en 1958, représente une avancée majeure dans le domaine de l'intelligence artificielle. Conçu au Cornell Aeronautical Laboratory, cet algorithme visait à modéliser le processus d'apprentissage humain en s'inspirant des réseaux neuronaux biologiques. Il s'agissait du premier modèle informatique capable d'apprendre à partir de l'expérience, marquant ainsi une étape cruciale vers le développement de machines intelligentes.

⚙️ Fonctionnement fondamental

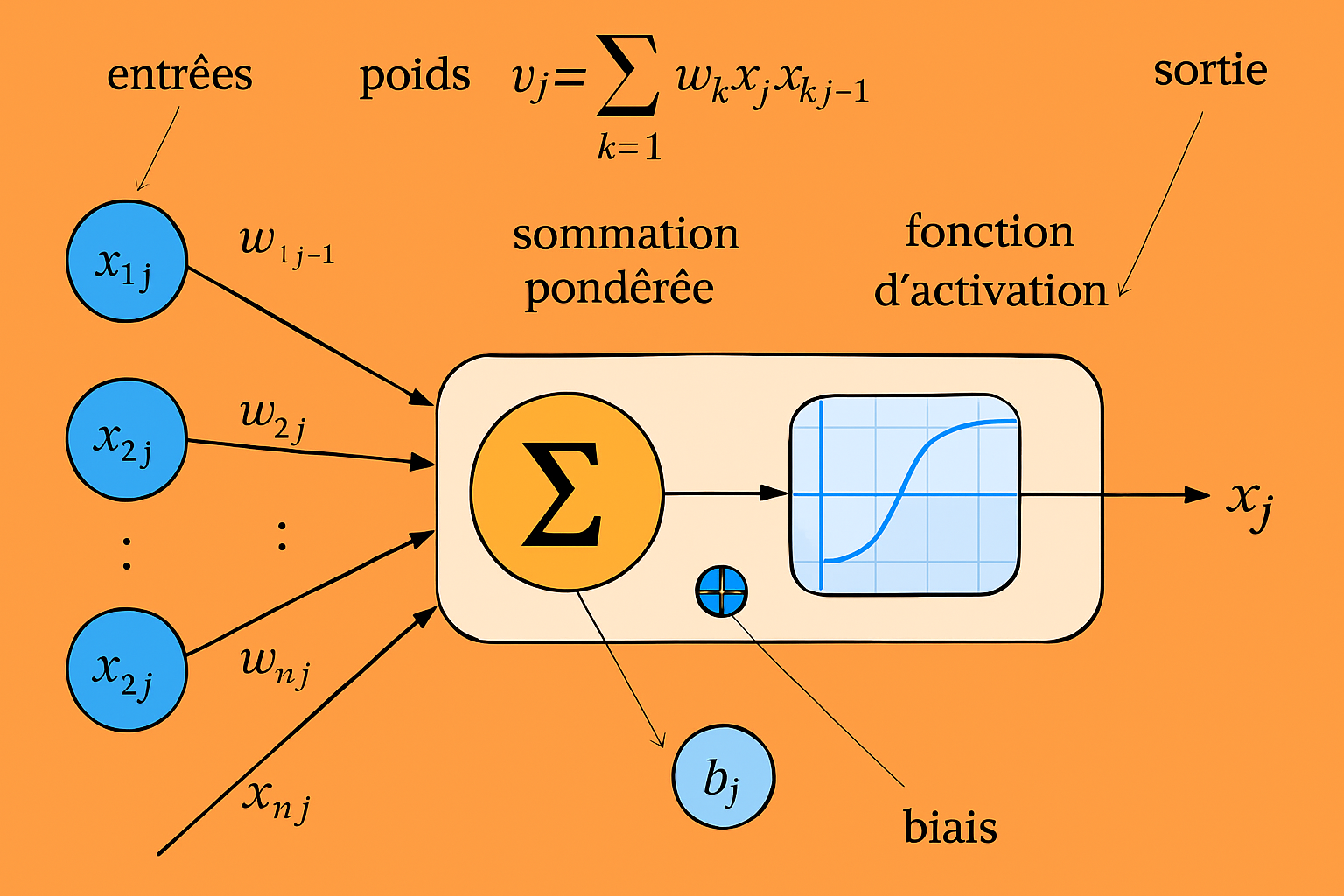
Le perceptron est un classificateur binaire qui prend des décisions en calculant une somme pondérée de ses entrées, ajoutant un biais, puis appliquant une fonction d'activation. Cette structure simple permet au perceptron de distinguer entre deux classes linéairement séparables. Cependant, cette simplicité implique également des limitations, notamment l'incapacité à résoudre des problèmes non linéairement séparables.
Imaginez le perceptron comme une cellule nerveuse artificielle qui :

1. Reçoit des signaux d'entrée (comme un neurone reçoit des neurotransmetteurs)
2. Pondère chaque signal par son importance (comme la force d'une synapse)
3. Intègre ces signaux pondérés
4. Déclenche une sortie binaire si l'activation dépasse un certain seuil (comme un potentiel d'action)

Analogies Biologiques

Le perceptron s'inspire du neurone biologique, recevant des signaux, les traitant et produisant une sortie. Néanmoins, tout comme un neurone isolé ne peut pas effectuer des tâches complexes, un perceptron simple est limité aux problèmes linéaires. Cette limitation a été mise en évidence par Minsky et Papert en 1969, qui ont démontré que le perceptron ne pouvait pas résoudre des problèmes tels que la fonction XOR.
En effet, chaque composant du perceptron trouve son équivalent en neurobiologie :

• Entrées (x₁, x₂,...) : Potentiels postsynaptiques
• Poids (w₁, w₂,...) : Efficacité synaptique
• Fonction d'activation : Mécanisme de génération des potentiels d'action
• Biais (b) : Seuil d'excitabilité du neurone

Figure 1. Architecture conceptuelle d'un perceptron montrant les entrées, les poids, le biais et la fonction d'activation.

🏗️ Vers des architectures plus complexesl

Pour surmonter ces limitations, les chercheurs ont développé des architectures multicouches, connues sous le nom de perceptrons multicouches (MLP). En empilant plusieurs couches de perceptrons, ces réseaux peuvent modéliser des relations non linéaires complexes, ouvrant la voie à des avancées significatives dans des domaines tels que la reconnaissance d'images et le traitement du langage naturel.

Fonctionnement Conceptuel

En effet, Le perceptron prend des décisions simples selon ce processus :

1. Réception des entrées : Des données (valeurs numériques) arrivent par plusieurs canaux
2. Pondération : Chaque entrée est multipliée par un "poids" qui en ajuste l'importance
3. Sommation : Toutes ces valeurs pondérées sont additionnées avec un terme de biais
4. Décision :
   • Si la somme dépasse un seuil → Sortie = 1 ("oui")
   • Sinon → Sortie = 0 ("non")

Capacités et Limites

Un perceptron unique peut apprendre à reconnaître des motifs linéairement séparables. Par exemple :

• Décider si un point est au-dessus ou en-dessous d'une ligne
• Classer des mots comme "positifs" ou "négatifs" basé sur certains critères
• Reconnaître des formes géométriques simples

Mais il échoue sur des problèmes non-linéaires comme la fonction XOR (ou exclusif), ce qui a mené au développement des réseaux multicouches.

Origines et Contexte Historique

Le perceptron a été développé dans le contexte des premières recherches en cybernétique et intelligence artificielle, influencé par :

• Le modèle de neurone formel de McCulloch-Pitts (1943)
• La théorie de l'apprentissage de Hebb (1949)
• Les premiers ordinateurs analogiques

Rosenblatt a conçu le perceptron non seulement comme un modèle mathématique, mais aussi comme un dispositif physique (le Mark I Perceptron) capable d'apprendre à reconnaître des formes visuelles simples.

Formalisation Mathématique

Maintenant que le concept est clair, examinons sa formulation mathématique :

\[ f(\mathbf{x}) = \begin{cases} 1 & \text{si } \sum_{i=1}^n w_i x_i + b > 0 \\ 0 & \text{sinon} \end{cases} \]

Où :

• \(\mathbf{x}\) : Vecteur des entrées
• \(\mathbf{w}\) : Vecteur des poids (à apprendre)
• \(b\) : Biais (seuil d'activation)
• \(f\) : Fonction d'activation (étape binaire)

Algorithme d'Apprentissage

Le perceptron apprend par correction d'erreurs :

1. Initialiser les poids aléatoirement
2. Pour chaque exemple d'entraînement :
   • Calculer la prédiction
   • Comparer à la vraie réponse
   • Ajuster les poids si nécessaire :
     \[ \Delta w_i = \alpha (y - \hat{y}) x_i \]
3. Répéter jusqu'à convergence

Bien que le perceptron ait connu des critiques et des périodes de désintérêt, il a jeté les bases de l'apprentissage profond moderne. Les concepts introduits par Rosenblatt continuent d'influencer les recherches actuelles en intelligence artificielle, soulignant l'importance de cette contribution historique.

Références

• Rosenblatt, F. (1958). The Perceptron: A Probabilistic Model for Information Storage and Organization in the Brain. Psychological Review.
• Bishop, C. (2006). Pattern Recognition and Machine Learning. Springer.
• Goodfellow, I., et al. (2016). Deep Learning. MIT Press.