Leçon 6 : Statistiques Fondamentaux
Leçon 6 : Statistiques Fondamentaux
Approche professionnelle pour futurs data scientists
La Moyenne Arithmétique
La moyenne arithmétique est un nombre qui représente une valeur « centrale » ou « typique » d’un ensemble de données. Elle est souvent utilisée pour résumer ou comparer des quantités.
| Symbole | Nom | Rôle | Type | Exemple |
|---|---|---|---|---|
| \(\bar{x}\) | Moyenne | Estimateur central | Statistique descriptive | Note moyenne d'une classe |
| \(n\) | Taille échantillon | Facteur de normalisation | Entier positif | Nombre d'étudiants |
| \(\sum\) | Sommation | Agrégation des valeurs | Opérateur | Total des notes |
| \(x_i\) | Valeur individuelle | Point de données | Variable quantitative | Note d'un étudiant |
Pyramide de Compréhension
Niveau 1 (Base) : La moyenne est la somme divisée par le nombre d'éléments.
Niveau 2 (Interprétation) : Centre de gravité du dataset, minimise les écarts quadratiques.
Niveau 3 (Expert) : Estimateur non biaisé de l'espérance quand \(n \to \infty\) (Loi des Grands Nombres).
Applications Professionnelles
Data Science : Normalisation des features, calcul de KPI
Finance : Rendement moyen d'un portefeuille
Contrôle Qualité : Suivi de la moyenne du processus
Attention : Sensible aux outliers (préférer la médiane pour données asymétriques)
⚠️ Attention !
La moyenne peut être influencée par des valeurs très grandes ou très petites (on les appelle des valeurs extrêmes ou outliers).
🧪 Exemple :
Prenons : 10, 10, 10, 10, 100
👉 La moyenne est 28, alors que la majorité des valeurs sont autour de 10.
Donc la valeur 100 fausse un peu la moyenne.
La Variance
La variance est une mesure de dispersion. Elle indique à quel point les valeurs d’un ensemble de données s’éloignent de la moyenne (ou moyenne arithmétique).
Autrement dit, plus la variance est grande, plus les données sont dispersées autour de la moyenne.
Plus elle est petite, plus les données sont concentrées autour de la moyenne.
📦 Exemple simple
Supposons que tu as les notes suivantes :
5, 7, 9, 10
Calcul de la moyenne :
Calcul des écarts à la moyenne au carré :
Calcul de la variance :
🧾 Donc, la variance = 3.6875
📌 Remarques importantes
- Unité : La variance est dans le carré de l'unité de mesure (si les notes sont sur 20, la variance est en "points²").
- Pour cette raison, on utilise souvent l'écart-type (la racine carrée de la variance) pour revenir à l'unité de départ.
Formule de la Variance
| Symbole | Nom | Rôle | Type | Exemple |
|---|---|---|---|---|
| \(s^2\) | Variance | Mesure de dispersion | Statistique descriptive | Variabilité des rendements |
| \((x_i - \bar{x})\) | Écart à la moyenne | Déviation individuelle | Variable centrée | Écart à la cible |
| \(^2\) | Carré | Élimine la direction | Opérateur | Amplifie les grands écarts |
Pyramide de Compréhension
Niveau 1 : Moyenne des carrés des écarts à la moyenne.
Niveau 2 : Second moment centré, mesure la variabilité absolue.
Niveau 3 : Base du calcul des intervalles de confiance (Théorème Central Limite).
Visualisation : Dans une distribution normale, 68% des données sont dans ±1σ, 95% dans ±2σ
Applications Professionnelles
Risk Management : Calcul de la volatilité (σ = √s²)
Machine Learning : Feature selection (éliminer les variables peu variables)
Contrôle Qualité : Calcul des capabilités processus (Cp, Cpk)
Théorème de Bayes
Le théorème de Bayes est un pilier fondamental des probabilités conditionnelles. Il permet de mettre à jour une probabilité initiale (appelée probabilité a priori) en fonction de nouvelles informations (appelées preuves ou évidences).
🔷 Exemple simple (test médical)
Imaginons un test pour une maladie rare :
\[ P(\text{Malade}) = 0.01 \] (1% de la population est malade)
\[ P(\text{Test}+|\text{Malade}) = 0.99 \] (le test est positif dans 99% des cas chez les malades)
\[ P(\text{Test}+|\text{Pas Malade}) = 0.05 \] (5% de faux positifs)
❓ Question :
Si une personne a un test positif, quelle est la probabilité qu'elle soit réellement malade ?
Étapes :
1. Probabilité que le test soit positif :
2. Appliquer Bayes :
✅ Résultat : Même si le test est positif, il n'y a que 16,7% de chances que la personne soit réellement malade.
Cela peut paraître contre-intuitif, mais c'est le pouvoir du théorème de Bayes !
Formule de Théorème de Bayes
| Symbole | Nom | Rôle | Type | Exemple |
|---|---|---|---|---|
| \(P(A|B)\) | Probabilité a posteriori | Croyance mise à jour | Probabilité conditionnelle | P(Maladie|Test+) |
| \(P(B|A)\) | Vraisemblance | Modèle génératif | Fonction | P(Test+|Maladie) |
| \(P(A)\) | Probabilité a priori | Croyance initiale | Probabilité marginale | Prévalence maladie |
| \(P(B)\) | Évidence | Facteur de normalisation | Probabilité marginale | P(Test+) |
Pyramide de Compréhension
Niveau 1 : Formule de mise à jour des probabilités.
Niveau 2 : Fondement de l'inférence bayésienne.
Niveau 3 : Cadre général d'apprentissage à partir de données.
Applications Professionnelles
Diagnostic Médical : Calcul de la valeur prédictive d'un test
Spam Filtering : Classificateur Naive Bayes
Risk Assessment : Mise à jour des probabilités de défaut
A/B Testing : Approche bayésienne vs fréquentiste
Distribution Normale
🔍 Qu'est-ce que la distribution normale ?
C'est une distribution continue qui décrit comment les valeurs d'une variable aléatoire sont réparties. Elle est souvent utilisée pour modéliser des phénomènes naturels comme :
- La taille des individus
- Les erreurs de mesure
- Les scores aux examens
- La pression sanguine
📈 Forme de la distribution normale
Elle est représentée par une courbe en cloche symétrique, centrée sur la moyenne (μ). Cette courbe est :
- Symétrique autour de la moyenne
- Les valeurs proches de la moyenne sont plus fréquentes
- Les valeurs extrêmes sont rares
📐 Paramètres importants
La distribution normale est entièrement définie par deux paramètres :
| Symbole | Nom | Rôle |
|---|---|---|
| μ | Moyenne | Centre de la distribution (le pic de la courbe) |
| σ | Écart-type | Mesure de la dispersion des données autour de la moyenne |
🧠 Loi normale standardisée
C'est une loi normale particulière où :
- $\mu = 0$
- $\sigma = 1$
On peut transformer une valeur normale en valeur standardisée (score Z) :
Cela permet d'utiliser des tables de la loi normale standardisée pour calculer des probabilités.
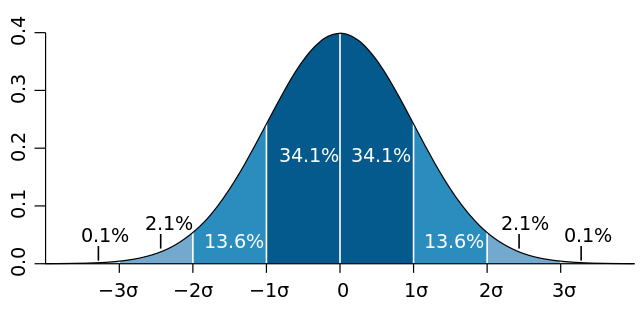
🎯 Règle empirique des 68-95-99.7%
Pour une distribution normale :
- 68% des valeurs sont dans l'intervalle [μ - σ, μ + σ]
- 95% des valeurs sont dans [μ - 2σ, μ + 2σ]
- 99.7% des valeurs sont dans [μ - 3σ, μ + 3σ]
C'est ce qu'on appelle la règle des 3 sigmas.
⚖️ 7. Propriétés importantes
- Symétrique par rapport à la moyenne
- Médiane = Moyenne = Mode
- Densité maximale au centre
- Les queues décroissent exponentiellement
📊 Deux (2) Exemples
Exemple 1 : taille d'une population
Si la taille moyenne est de 170 cm avec un écart-type de 10 cm :
Entre 160 cm et 180 cm (μ ± σ), on trouve environ 68% de la population.
Plus une personne s'éloigne de 170 cm, plus elle devient rare statistiquement.
Exemple 2 : score d'un test
Un score de 60 correspond à :
Cela signifie que cette personne est dans le top ~2.5% des scores (car P(Z > 2) ≈ 2.5%).
Interprétation : Seulement 2.5% des participants ont obtenu un score supérieur à 60.
🔢 Équation de la distribution normale
La fonction de densité de probabilité (PDF) de la loi normale est :
| Symbole | Nom | Rôle | Type | Exemple |
|---|---|---|---|---|
| \(\mu\) | Moyenne | Paramètre de position | Réel | Centre de la distribution |
| \(\sigma\) | Écart-type | Paramètre d'échelle | Réel positif | Dispersion des données |
| \(e\) | Exponentielle | Décroissance rapide | Fonction | ≈ 2.71828 |
| \(\pi\) | Pi | Constante de normalisation | Constante | ≈ 3.14159 |
Pyramide de Compréhension
Niveau 1 : Distribution en cloche symétrique.
Niveau 2 : Solution de l'équation de diffusion (physique statistique).
Niveau 3 : Distribution maximisant l'entropie pour variance fixée.
Applications Professionnelles
Contrôle Qualité : Cartes de contrôle (Shewhart)
Finance : Modélisation des rendements (hypothèse normale)
Machine Learning : Hypothèse de bruit gaussien en régression
Tests Statistiques : z-test, t-test, ANOVA
Commentaires
Enregistrer un commentaire